leetcode

之前做很多题的时候还没有搭blog，随便记录点后面做的简单题。

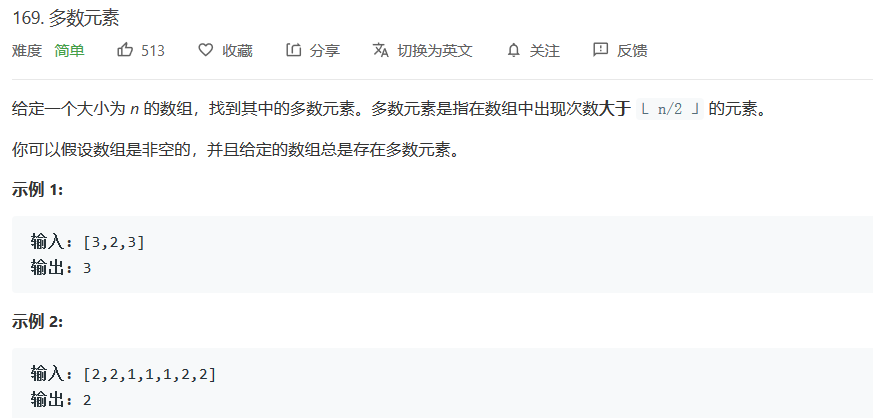
摩尔投票

个人总结：

在一群以小队为组的战争中， 2个遇到若不是同队的就双方阵亡，若2个人是同队的就结合起来。这样一直下去，最后留下来的人，将是这场战争中最多的人的小队的。该算法可以解决计算一个数组中出现次数最多的元素。( 从第一个数开始count=1，遇到相同的就加1，遇到不同的就减1，减到0就重新换个数开始计数，总能找到最多的那个 )

int majorityElement(int* nums, int numsSize)
{
  int count = 0, ans = 0;
    
  for(int i = 0; i < numsSize; i++)
  {
     if(nums[ans] == nums[i])
       count++;
     else
       count--;
      
     if(count == 0)
       ans = i+1;

     if(count > numsSize/2)
       break; 
  }
    
  return nums[ans];
}

动态规划

将一个问题，分成若干个的子问题解决

dp[i]表示nums[0]到nums[i]，含nums[i]的最长上升子序列；
如果nums[j] < nums[i],就dp[i]=max(dp[i],dp[j]+1)
每次保存最大长度res=max(res,dp[i]) ////因为最后一个元素nums[n]，不一定在最长子序列中

如[10,9,2,5,3,7,101,6]
[10,9,2,5,3,7,101,6],dp[0]=1
[10,9,2,5,3,7,101,6],dp[1]=1
[10,9,2,5,3,7,101,6],dp[2]=1
[10,9,2,5,3,7,101,6],dp[3]=dp[2]+1 //res=2
[10,9,2,5,3,7,101,6],dp[4]=dp[2]+1 //res=2
[10,9,2,5,3,7,101,6],dp[5]=dp[3]+1 //res=3
[10,9,2,5,3,7,101,6],dp[6]=dp[5]+1 //res=4
[10,9,2,5,3,7,101,6],dp[7]=dp[4]+1 //res=4

int lengthOfLIS(int* nums, int numsSize)
{
  if(numsSize == 0)
  return 0;
    
  int max = 1;
  int dp[numsSize];

  for(int i = 0; i < numsSize; i++)
  {
      dp[i] = 1;
      for(int j = 0; j < i; j++) 
          if(nums[i] > nums[j])
              dp[i] = dp[i] > dp[j]+1 ? dp[i]:dp[j]+1;
      if(dp[i] > max
         max = dp[i];
  } 

  return max;
}

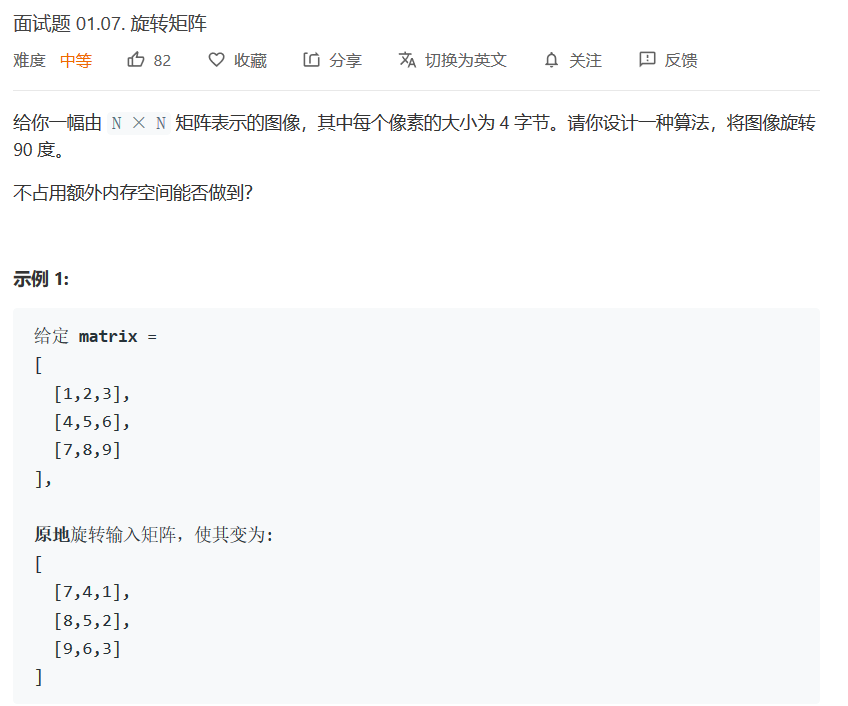
旋转矩阵

对于矩阵中每一行都旋转90°，在不占用额外空间情况下。可以先把整个矩阵转置一下，再左右的2的数交换一下位置即实现。

题解:

void rotate(int** matrix, int matrixSize, int* matrixColSize)
{
	for(int i = 0; i < matrixSize; i++)
	{
		for(int j = i+1; j < *matrixColSize; j++)
		{
			int temp = matrix[i][j];
			matrix[i][j] = matrix[j][i];
			matrix[j][i] = temp;
		} 
	} 
	
	int mid = matrixSize >> 1;
	for(int i = 0; i < matrixSize; i++)
	{
		for(int j = 0; j < mid; j++)
		{
			int temp = matrix[i][j];
			matrix[i][j] = matrix[i][matrixSize-j-1];
			matrix[i][matrixSize-j-1] = temp;
		}	 
	}
}

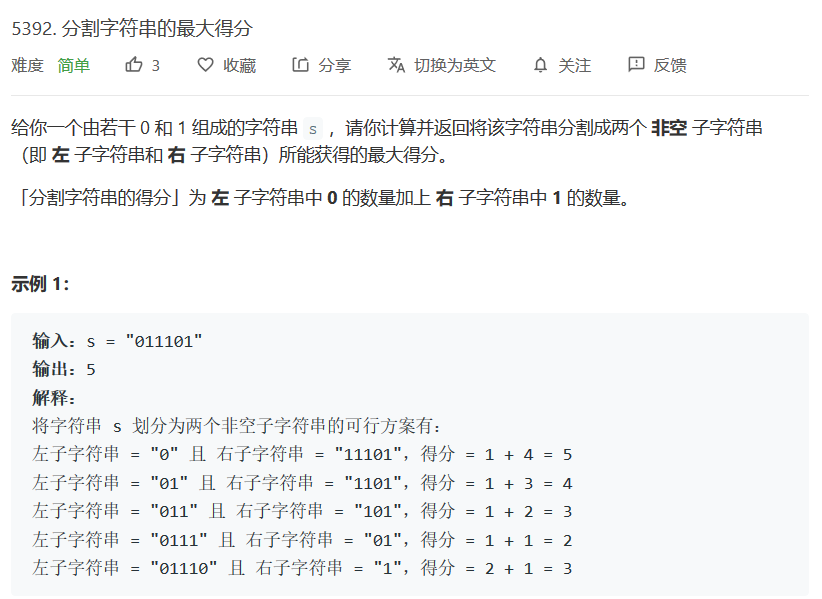
分割字符串

一道题不难的题，但是觉得思想应该记一下。

第一个思路是: 只管左边, 统计左边0和1出现的次数, 只要从左到右循环，0出现的次数与1出现的次数之差比第一个比开始大，那么我们的确定分割的位置就可以往后移。循环一遍，找到了位置，再分别相加。

第二个思路: 先把所有的 1 都统计出来，再左往右循环，只要是字符0就加1，字符1就减1。第二个思路代码: C语言

int maxScore(char * s)
{
	int ans = 0, count = 0;
	
	for(int i = 0; i < strlen(s); i++)
	count += (s[i] == 49 ? 1 : 0);
	
	for(int i = 0; i < strlen(s); i++)
	{
		count += (s[i] == 0 ? 1 : -1);
		
		ans = (ans > count ? ans : count);
	}
	
	return ans;
}

python3

class Solution:
    def maxScore(self, s: str) -> int:
        count = s.count('1')
        ans = 0
        for i in s[:-1]:
            if i == '0':
                count += 1
            else:
                count -= 1
            ans = max(ans, count)
        return ans

最后, 同然的算法, python虽然方便,但是python在时间和空间复杂度上, 比C语言大好多.

异或运算

异或运算的运用, 对逆向分析有帮助.

首先异或运算的性质有.

交换律	a ^ b = b ^ a
结合律	(a ^ b) ^ c = a ^ (b ^ c)
对于任何数a	x ^ x = 0, x ^ 0 = x
自反性	a ^ b = c -> c ^ b = a

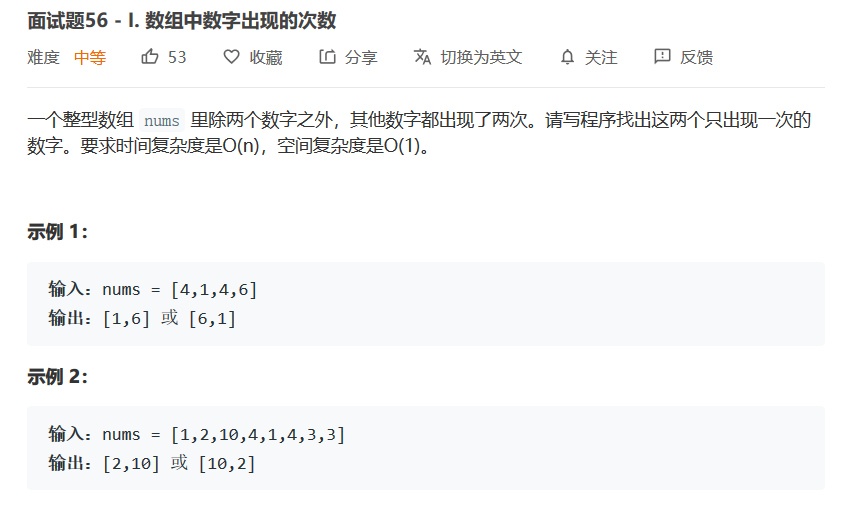
第一种题型: (要求是空间复杂度 0(1)，时间复杂度 0(n))

在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了2次。请找出那个只出现一次的数字。

思路一: 用数学的方法，首先让让数组中非重复的数字都相加后等2(sum(set(nums)))*2，然后让s该数组求和(sum(nums))，2者只差得到答案。

思路二：由异或运算的性质，我们让所有的元素异或运算，结果就是答案

第二种题型，是第一种的延伸。

int* singleNumbers(int* nums, int numsSize, int* returnSize)
{
	int sum = 0, flag = 0;
	int *ans = (int *)malloc(sizeof(int)*2);
	
    memset(ans, 0, sizeof(int)*2);
	for(int i = 0; i < numsSize; i++)
	sum ^= nums[i];    /有第一个题型, 我们知道最后结果是不相同两个数的异或结果.
	
	flag = (-sum)&sum;  /取sum的所有位中第一个为1的位.
	for(int i = 0; i < numsSize; i++)
	{
		if(flag & nums[i])   /将不相同的两个数进行分组, 依据上面计算的flag.
			ans[0] ^= nums[i];
		else
			ans[1] ^= nums[i]; 
	} 
	
    *returnSize = 2;
	return ans;
}

qsort的使用

可以自定义排序，比自己的写的快排快多了。int cmp(const void *a, const void *b);

这道题自己写的快排过不了，后面换用C库的qsort自定义排序就好了。

int m = 0;

int cmp1(const void *a, const void *b)
{
	return (*(int *)a-*(int *)b);
}

int cmp2(const void *a, const void *b)
{
	int *p = (int *)a;
	int *q = (int *)b;
	
	if(abs(*p-m) == abs(*q-m))
		return *p-*q;
	else
		return abs(*p-m)-abs(*q-m);
}
int* getStrongest(int* arr, int arrSize, int k, int* returnSize)
{
	 qsort(arr, arrSize, sizeof(int), cmp1);
	 m = arr[(arrSize-1)/2];
	 
	 qsort(arr, arrSize, sizeof(int), cmp2);
	 
	 *returnSize = k;
	 return arr;
}

总结：根据题目要求自定义排序方法，还是很灵活。